M17 能量最低原理和轨道能级

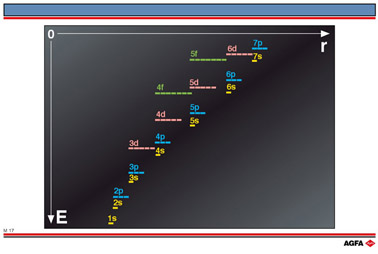
图 M17 表示轨道能级是r的函数(r为由核到电子的距离)，或者说，由小变大的整数主量子数n与能级(例如1s、2p 或5f)有关。主量子数n为整数，它通过以下表示式决定电子在允许轨道上的角量子数

[式中的整数 n 描述了氢原子发射光谱线系列的波长，见图 M09和M10的说明。]

原子中一个电子的能量可以用4个量子数来表征:

• 主量子数n，为整数;
  
• 角量子数l，取整数值0，1，2，3，⋯，(n-1);
  
• 磁量子数m，取整数值-l，-(l-1)，-(l-2)，⋯，0，⋯，(l-2)，(l-1)，l;
  
• 自旋量子数s，取值 +1/2 和- 1/2。可将电子看成像陀螺一样，绕轴顺时针和逆时针旋转。

泡利(Wolfgang Pauli 1900~1958)第一次提出这种填充轨道能级的方法。他在“排斥理论”中提出， 一个原子中不可能有两个电子的4个量子数完全相同。换句话说，在任一原子中，不可能有两个电子具有 完全相同的行为。如果认为氦原子处于最低能量状态，它的两个电子应该取相同的量子数n = 1、l = 0、m = 0。这意味着，按照泡利不相容原理，这两个电子的第四个量子数(自旋量子数)必不相同，即一个电子的自旋态为 +1/2，另一个的则为- 1/2。自旋相反的一对电子以如下符号表示:

按照洪特规则，电子先单独占据每一能级，然后才发生配对。

根据能量最低原理，可用的电子按轨道能级增加的顺序，成对填入可用的轨道中。主量子数n相同的轨道， 如2s和2p轨道，以及3s、3p和3d轨道，轨道能级按如下顺序升高:s< p< d< f.

一个特定电子层或电子亚层(具有相同主量子数和角量子数的一组轨道)中的所有轨道具有相同的能量。例如3个2p轨道的能量相同。

较高的能级可能不服从能量最低原理。例如，Ac为 7s² 6d¹而不是
7s² 5f¹，原因是各种能级间发生了相互交错。

参考文献：

C.E. Mortimer, ‘Chemistry’, Wadsworth Publishing
Company, Belmont, California.