POL22 聚合物的机械性能

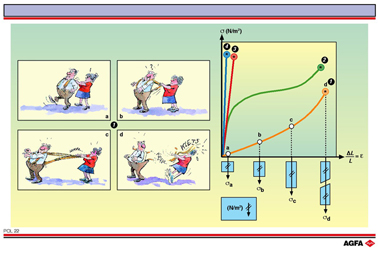
当聚合物用于特殊应用时，它的性能就起了很重要的作用。 其中机械性能是最重要的。这里我们指的是在拉伸作用下，聚合物表现出的变形性和流动性。在插图POL 22-1，2，3，4中，已经给出了一些性质。

这些曲线说明伸长率

是单位表面积上所受的力(即应力σ)的函数(σ 单位为N/m²)。

从这些曲线中可以推断出重要的性质，包括:

• 弹性模量E(由公式σ = e.E) 推导而来,给出了聚合物应变与应力的关系。这个系数由曲线开始时呈线性关系部分的斜率决定。
  

• 断裂应力(*)说明了破坏一个样品需要多大的力。
• 弹性伸长率给出了聚合物能够恢复到初始状态的最大伸长数值。

随着聚合物用途的不同，对它们的机械性能的要求也会发生改变。

我们提供几个例子:

- 人造橡胶(POL 22-1)
  在相对小的σ 值条件下，这些聚合物可以达到相当大的且能恢复形变的伸长率e (500%~1 000%)。
  一个典型的例子是1,2-反式聚异戊二烯:

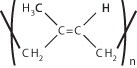
   在应力为2000 N/m²条件下，这种聚合物可以达到500%的 伸长率。

- 中间体类的聚合物(POL 22-2)
  在这一类物质中，我们可以找到一些性质介于橡胶和纤维之间的聚合物。聚乙烯是一个典型的代表。它是既柔软(在500 %伸长率时，模量E≈20 000 N/m²)又刚硬的材料。

- 纤维 (POL 22-3)
 能够作为纤维的聚合物可以承受很强的形变。它们的伸长率仅为10%~50%，具有很高的模量 (E > 35.000 N/m²)。
尼龙-66是此类聚合物的典型代表。

- 刚性的塑料 (POL 22-4)
在模量E为70000~350000 N/m²时，这种聚合物表现出极强的抵抗形变的能力(伸长率 e < 0.5 to 3%)。电木是一个典型的例子。