E17 模拟平衡的“水游戏”
|
目标:使用不同规格的管子，从一个量筒向另一个量筒中转移液体。可通过该模型直观地模拟平衡的很多方面，如模拟达到平衡所需时间，反应的动力学特征，浓度，反应速率，速率常数，温度的影响，平衡常数，转化度和外加变化对平衡的影响。 |
为了使学生对于化学平衡条件是如何产生和变化的有更好的理解，富有丰富想像力的老师们设计了一些直观模拟这个过程的方法。
我们介绍两种模拟该过程的方法:第一个很简单，很容易就可以说明清楚;第二个就更精细一些。
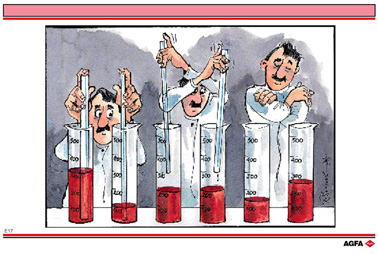
把相同长度但是直径不同的长玻璃管放在两个相似的500mL量筒中。量筒A(左边的)装有300mL水， 量筒B(右边的)装有100mL水。
同一个人可以借助玻璃管用一只手将液体从A转移到B中，而用另一只手将液体从B移到A中。在 “移液”过程中，每一个玻璃管都要绝对垂直的拿着，其管口端需要接触量筒底部。在每一次转移之前，要等玻璃管尽可能的被充满后，再用手指堵住顶端。
通过这种转移，两个量筒中的液面发生了变化。A的液面开始时较高，但是A的内径是B的2倍。这样A中的液面就会下降，而B中的液面就会升高。随着转移次数的增加，两个量筒中的液面变化就会越来越小。当转移次数到一定数值(约40)时，从宏观上看，液面就不再变化。这时尽管继续转移，液面仍保持不变。
这清楚地表明液面已经达到了平衡—— 一个动力学平衡。
除了化学平衡条件受动力学控制的性质之外，一个平衡反应的其他一些方面的性质也可依次通过这个模型来模拟。
B型的反应，这个数值对应于在平衡态时两液面的高度比:he (A) /he (B)。
可逆性:在相同的反应条件下，化学反应无论是从反应物一方(或为优势方)开始，还是从产物一方(或为优势方)开始均得达到化学平衡。这个模拟方法关键是要改变起始液面高度但是保持两量筒中液面总高度恒定，也就是只要使用相同的管子，就可以达到同一平衡液面了。
B。
