E06 - E07 - E08 平衡定律

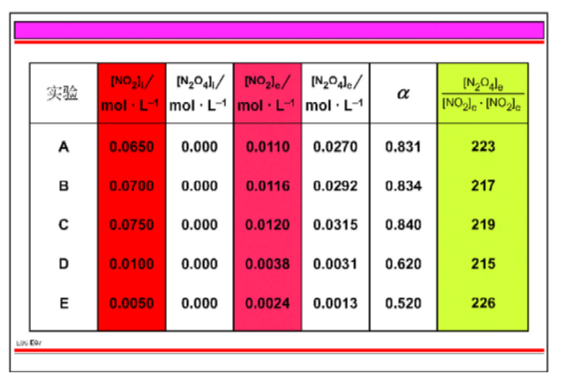
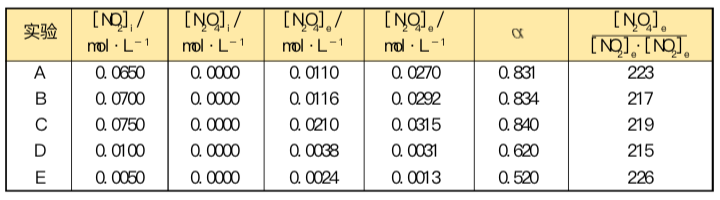
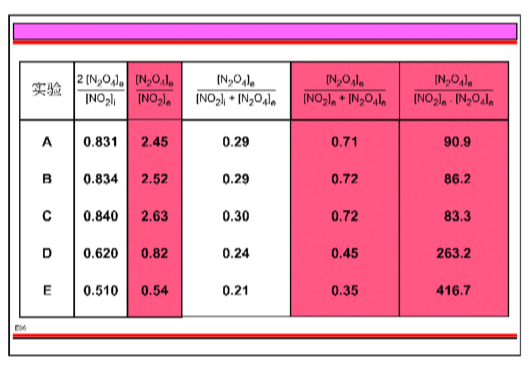
图E06给出在25°C下五组不同NO₂二聚化实验A、B、C、D、E中NO₂和N₂O₄的初始浓度和平衡浓度:

实验A、B、C 的结果已经在图例E01中说明了。在实验A、B、C中NO₂初始浓度很相近，然而在实验D和E中却少得多。

五个实验中NO₂的转化度a 随NO₂浓度不同而异。一个特定平衡反应的转化度为什么会很不同呢? (从不同初始浓度出发确会得到这些平衡混合物，但是对这五个实验最后的平衡温度是相同的。)

考虑不同的NO₂初始浓度，能不能发现在25°C下控制NO₂二聚化平衡反应的一个基本关系?

S总的来说，科学家一直在寻找用来解释这些观察现象的根本关系，从而进一步发现具有更广范围普适性的基本规律。人们不得不思考去寻找一种控制着重力、库仑力、核力和宇宙力的基本规律，从而推演出一个蕴藏在这众多力之间的定律。

正是这样，在19世纪下半叶许多杰出科学家，就像Van't Hoff、Guldberg和Waage，都在思考化学平衡现象中存在基本关系的可能性，能被用来预测在特定反应条件和反应物初始浓度下的平衡浓度和转化率。

经过反复试验，他们的实验和理论工作最终得到回报，他们发现了适用于众多领域的基本规律。

关系式的推导

是否存在一个基本量，能表现在特定条件下进行的某一确定的平衡反应的平衡混合物的所有可能特征?这个量不是转化率，因为它随NO₂初始浓度不同而变化，但可能是一个相关的表达式。

在图 E08 中，实验得到了五个可能的表达式:

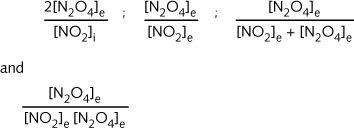
这些没有一个能使那五个实验得到一个常数值。
最后，经过反复试验，得到一个计算值在222附近变化的表达式:

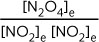
有关数据见图 E07，可用图 E07 来覆盖图 E06。

可能还有另一种关系式存在，或者是其中的一个变量(比如倒数或平方根)，但是上述这个关系确实存在。

这样，对于在一定温度下进行的均相体系的平衡反应，应用一个或多个关系式的变量都能推算出平衡常数，而不依赖于反应物和产物的初始浓度。

国际公认的关系式习惯写法是:
ð 将产物平衡浓度写在分子
ð 将反应物平衡浓度写在分母

这个表达式用平衡常数符号K_c 表示。对于 NO₂二聚化反应:

经过对众多平衡反应的广泛研究，对均相体系的平衡反应都可用通用方程式表示:

下面是通用表达式:

这个是从完整的反应方程式中很容易得到的一个简单表达式。

另一个例子

一边是Fe(III)离子和碘离子，另一边是Fe(II)离子和碘单质，能在水中建立起不同的平衡。两个都在图E03中展示，一个从反应物开始，另一个从产物开始。平衡常数的相应表达式是:

实际上，三氯化铁和碘化钾或者氯化亚铁固体和碘单质加到水中都能得到平衡混合物。

通用平衡定律或者平衡条件

对任何平衡反应，把平衡浓度代入相应的 K_c表达式都能得到相同的值。如果在相同反应温度下建立平衡，那么以上就都成立，而与混合物初始组成无关。

相反，一个反应混合物在平衡状态下是否确定，通过以下方法确定:把反应物和产物浓度代入适当的 Kc表达式 ，并比较得到的值和在一定温度下此反应已知的Kc值。

注意：

平衡定律或者平衡常数是从反应的热力学最先推出的，平衡常数Kc的数值主要依赖于反应物和产物的特性(见图E27)。

反应速率和反应机理是反应动力学的范畴。它们与Kc表达式和Kc值没有任何关系。假定哪些不切实际的反应方程式都能得到一个Kc表达式是简单化和轻率的。