M14 1s 轨道

1924年，德布罗意(Louis de Broglie)第一次提出电子具有波动性。一个光子的能量E与其频率成正比:

E = h
其中 h 为普朗克常数。

根据爱因斯坦方程(E=mc2)，德布罗意提出以下公式来计算一个电子的波长:

λ = h/(mv)
其中h为普朗克常数;v 为电子速率。

公式表示:

波动性 = 常数 / 粒子性

在此，德布罗意为电子既赋予了粒子性，又赋予了波动性。此后，在1926年，E·薛定谔将这个模型用于表达电子波动性的微分方程中。

薛定谔波动方程只有在确定的条件下才能解出，这些条件代表的是某些完全确定的电子状态。我们可以从物理学角度来理解:如果把正在绕核运动的电子当成波处理，为了避免发生破坏性的干扰，波长的整数倍必须与绕行的圆周长相匹配。

通过解析氢原子中电子的薛定谔波动方程可得到一系列波函数。每个波函数对应电子的一个特定能级及其位置。每个波函数实际上描述了一个原子轨道。

波的强度与其振幅的平方成正比。波函数是一种振幅函数。与电子的密度，即在空间某点发现电子的概率P成正比。在空间某特定点发现电子的概率与该点的电子云成正比。

对一个处于n=1状态的电子，即1s轨道上的电子，电子密度在核附近达到最大值，但在核处减小为零。超过最大值的距离，离核越远电子密度越小。

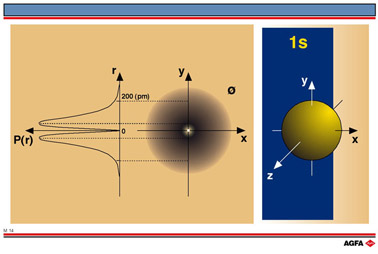
图M14的左边图形为径向概率P(r)曲线，即在离核某确定距离处发现一个电子的概率。

图M14的中间部分是1s轨道的轮廓图(即用电子云表示的截面图)。离核距离大约200 pm处的虚线划出了概率为90%的区域。在核与该划定界限之间，发现电子的概率为90%。图右边部分表示的是1s轨道的界面。将概率相同的点连接起来，得到一个球面。在这个球面所包含的体积内，发现一个电子的机会为90%。